Japanese Multiplication Trick is the Best First Thing You’ll Learn in 2021



By Carl Samson
If you’re down to learn something cool and quick this early in the year, a multiplication “trick” attributed to the Japanese may be your best bet.
The graphic method, which makes use of sticks and dots, has gone viral on TikTok since user @mathswithmisschang posted it back in August.
While Miss Chang — among others — traces the system back to Japan, some say it actually originated from China, the Vedics or elsewhere.
In her TikTok video, Miss Chang tries to multiply factors 42 and 21.

To solve this, one must first convert individual digits into sticks and lay them diagonally on top of each other.

Open curves are then drawn before the sticks intersect on both the left and right sides.

Finally, dots are marked where the lines intersect.

The answer is revealed by counting the dots on each space separated by the curves.
In the case of the above, it’s 882.

In a more recent video, Miss Chang tries to multiply three-digit factors using the same system. The graphic ends up with four curves and five spaces.
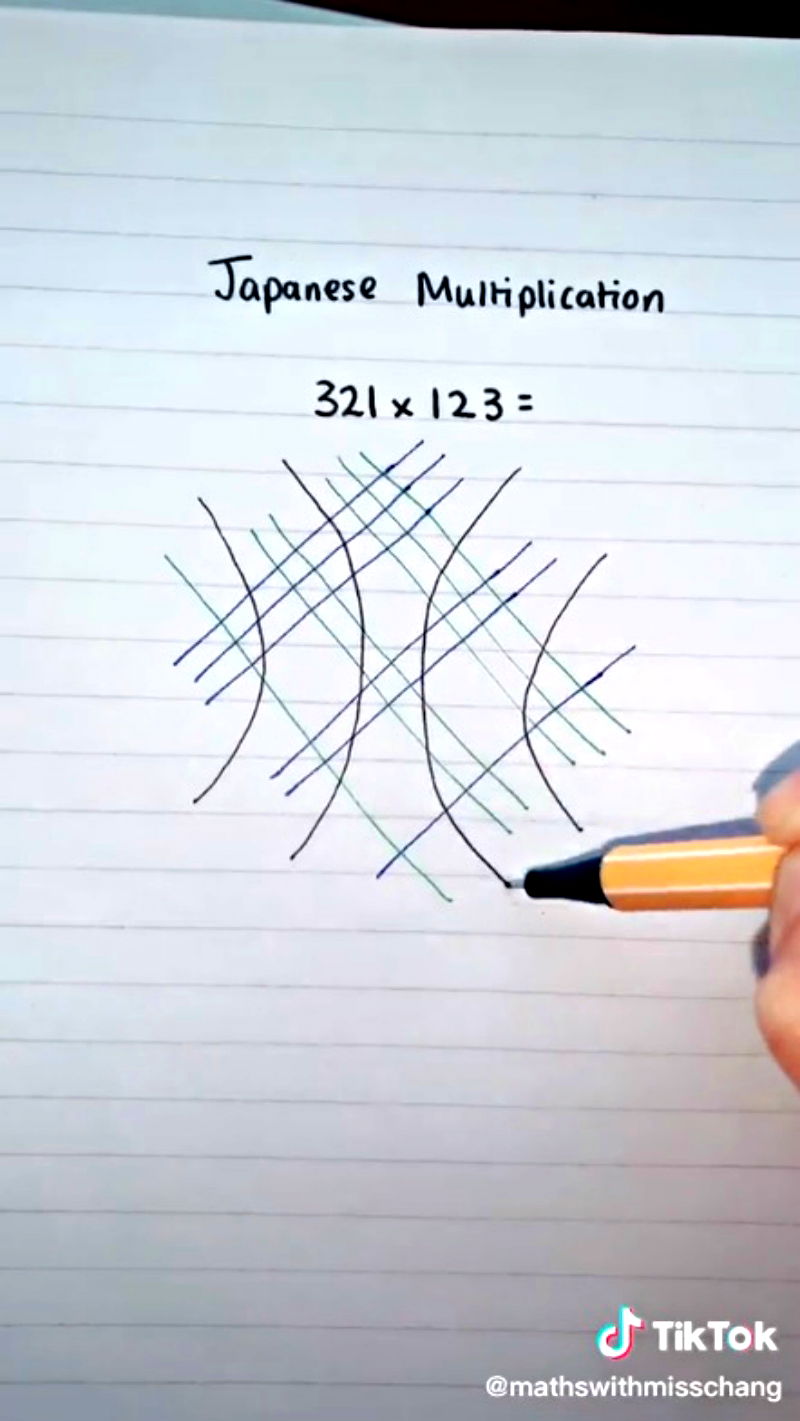
This time though, she shows how to deal with an “excess” digit. Interestingly, it appears to follow the same principle of “carrying over” in traditional multiplication.

The “trick” looks undeniably elegant when dealing with smaller digits, but it quickly falls apart when multiplying 9 and 8, for instance.
That’s probably because the method was not originally designed to appear cool or impressive. As Caroline Delbert puts it in a Yahoo article:
“People working as builders or doing business often didn’t know how to read and write, let alone have something to write on at hand. If they could break problems into actual physical pieces they could arrange and count, that was easier, faster, and required less brute force memorization even in the short term.”
Nonetheless, the method appears to be a hit on TikTok. And it surely won’t hurt to learn something new.
“This is my favorite method. I’ve literally used this every time,” one user wrote in the comments.
Still, some found it confusing.
“What is this? I don’t understand it at all,” one noted.
Feature Image Screenshots via @mathswithmisschang
Share this Article
Share this Article